
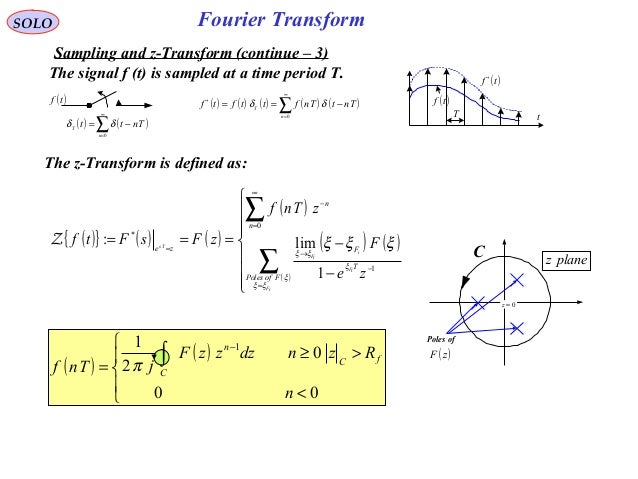
It is a linear transform – If g(t) and h(t) are two Fourier transforms given by G(f) and H(f) respectively, then the Fourier transform of the linear combination of g and t can be easily calculated.Some of the properties of Fourier transform include: Where F(k) can be obtained using inverse Fourier transform. The Fourier transform of a function f(x) is given by:
#FOURIER TRANSFORM SERIES#
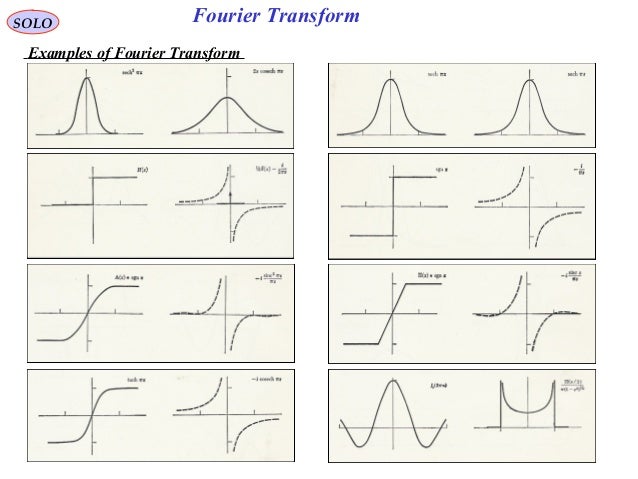
The Fourier transform helps in extending the Fourier series to non-periodic functions, which allows viewing any function as a sum of simple sinusoids. This term can also be applied to both the frequency domain representation and the mathematical function used.

The Fourier transform is also called a generalization of the Fourier series. The absolute value of the Fourier transform represents the frequency value present in the original function and its complex argument represents the phase offset of the basic sinusoidal in that frequency.
The result produced by the Fourier transform is a complex valued function of frequency. The Fourier transforming lens has a focal length of 100 mm.The Fourier transform is a mathematical function that decomposes a waveform, which is a function of time, into the frequencies that make it up. This effect can be seen in the SLM drive levels shown in Fig. In order to increase brightness–albeit while reducing the effective resolution–each point on the input function is represented by four pixels on the SLM to increase brightness, and a Nyquist-frequency chequerboard is used to carry the OFT away from the zero-order point to avoid interference. ( 2c) (to within a rotation, which represents an arbitrary global phase delay). If we could perform the Fourier transform optically, we would escape the \(\) accessible states in an optimised polariser configuration provide the required modulation scheme, as shown in Fig. Historical approaches include: iterative algorithms 12 which are too slow for a Fourier coprocessor direct methods based on including a reference in the input plane 13 and of course interferometry. While a camera sensor can straightforwardly measure the magnitude, determining the phase is a venerable problem.
#FOURIER TRANSFORM FULL#
However, using this phenomenon to evaluate a complex-to-complex Fourier transform requires full complex control of the light at the input spatial light modulator (SLM), and measurement of the complex amplitude across the focal plane at the output. The Fourier transform at the core of coherent optics is straightforwardly implemented with a classic 2f system 11. Specifically, we consider the natural application of the Optical Fourier Transform (OFT): replacing the Discrete Fourier Transform (DFT), as normally implemented by a Fast Fourier Transform (FFT) algorithm, with a dedicated optical coprocessor. However, it still potentially offers significant advantages over electronic methods when used appropriately 8, 9, 10. Despite this rich and prodigious history, OIP has often failed to compete with the formidable progress of digital electronic computers 7. Historically, optical information processing (OIP) has manifested itself in many imaginative–and some successful–ways: from image processing 1, 2, 3 and pattern matching 4, to numerical equation solving 5 and even to implementing a general purpose digital computer 6.
This method could unlock the potential of the optical Fourier transform to permit 2D complex-to-complex discrete Fourier transforms with a performance that is currently untenable, with applications across information processing and computational physics. Performing larger optical Fourier transforms requires higher resolution spatial light modulators, but the execution time remains unchanged. By appropriately decomposing the input and exploiting symmetries of the Fourier transform we are able to determine the phase directly from straightforward intensity measurements, creating an optical Fourier transform with O(n) apparent complexity.

Efficiently extracting the phase from the well-known optical Fourier transform is challenging. By implementing the Fourier transform optically we can overcome the limiting O(nlogn) complexity of fast Fourier transform algorithms. We propose and demonstrate a practical method to optically evaluate a complex-to-complex discrete Fourier transform. The Fourier transform is a ubiquitous mathematical operation which arises naturally in optics.


 0 kommentar(er)
0 kommentar(er)
